Y2 3 N z = 2 = 3 0 2= 4 = 5 Z = 6 b I have the following twovariable function f(x,y) = exp(x^2(y1)^2) And I need to compute/sketch the level curves for exp(1), exp(1/4) and 1 I'm not sure how to go about this, I'm not even sure what the range is so this is a bit daunting AnyLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c

Mth 254 Test 2 Review Key 0704 Spot Pcc Mth 254 Test 2 Group Review Key Page 2 Of 9 5 I Probably Pdf Document
Level curves of a function calculator
Level curves of a function calculator-Add a Calculator application to a TINspire document and enter the following Solving z = f(x;y) succeeded and there are two solutions which can be used to create lists of functions to plot the level curves Step 2 Graph z = f(x;y) and use the menu item Trace zTrace to determine theGiven w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3space Then on a level surface the temperature is




Level Curves For The Region Of The Potential Energy Surface With The Download Scientific Diagram
The function z = ¨ xy ¨ In17= Plot3D@Abs@xyD, 8x,1, 1 30, Mesh> False, AxesLabel> 8"x","y","z"Double checking my own approximation to the function for a solution to the inf circular potential well in QM 4 2326 years old level / Highschool/ University/ Grad student / Useful /Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the
Level curve calculator in Description DgFlick Edit Xpress STD DgFlick Edit Xpress is an easy to use photo correction tool You get basic editing tools like BCG, RGB, Level, Curve and advanced editing tools like Lasso, Chroma, Touchup, Highlighter, etc Batch editing feature lets you color correct 1000s of the photos in a single click Homework Statement I have this function of two variables f(x,y)=x^24xy^2 Where I have to compute the level curves for f(x,y)=3, 2, 1, 0, 1 Homework Equations The Attempt at a Solution So yeah well I know that I have to draw the following curvesHow to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 3
10 1655 60 years old level or over / Highschool/ University/ Grad student / Very / Purpose of use Sending completion To improve this 'Gamma function Calculator', please fill in questionnaire Age Under years old years old level 30 years old level 40 years old level 50 years old level 60 years old level or overFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andVideo Transcript {'transcript' "problem were sketching the level curve for the function F X Y is equal to X squared plus y squared for the given values have seen I've done so using decimals, the online calculator analogy to enter the equations that it did go to see entered the given values of C, and this would be the resulting graph"}




Contour Plot An Overview Sciencedirect Topics




Normal Distribution Calculator High Accuracy Calculation
2 Answers2 Active Oldest Votes 1 In your first example, the proper solution is y = ± k − x 2 You left out the plusorminus That is not a small thing there are usually two values of y for each x, and that greatly affects the plotting of the curves I would say that there is no single general method for finding level curves, in aThe calculator will find the inverse of the given function, with steps shown If the function is onetoone, there will be a unique inverse Your input find the inverse of the function $$$ y=\frac {x 7} {3 x 5} $$$ To find the inverse function, swap $$$ Calculus Calculus questions and answers Determine level curves of the function z = Iz?



Parent Functions And Their Graphs Video Lessons Examples And Solutions




The Economy Leibniz Isoprofit Curves And Their Slopes
Another example is the two variable realvalued function $f(x, y) = x^2 y^2$ which represents a hyperboloid The level curves generated by the planes $z = 1$, $z I am being asked to calculate level curves for the following equation f(x,y)=e^(2x^22y^2) but I do not know where to start Any adviceBy calculating derivatives Then you set the function as well as the derivative equal to zero Roots are solutions of the equation



Demand Curve Formula Economics Help



The Gradient And Directional Derivative
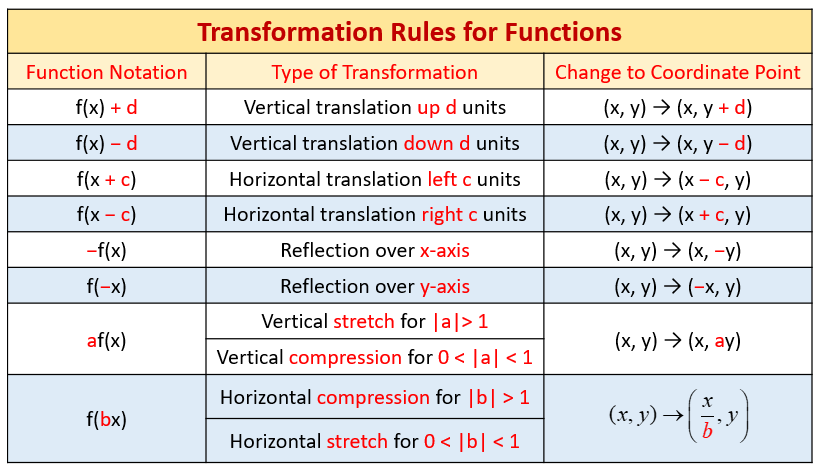
Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kLevel Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andJust add the transformation you want to to This is it For example, lets move this Graph by units to the top



Consider The Function F Y 4273 Easy Course Hero



Peak Voltage Calculator Electrical Engineering Electronics Tools
Get the free "Level Curves" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaA free graphing calculator graph function, examine intersection points, find maximum and minimum and much more This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyThis depends on the direction you want to transoform In general, transformations in ydirection are easier than transformations in xdirection, see below How to move a function in ydirection?




The Economy Leibniz Isoprofit Curves And Their Slopes



1
Use a graphing utility to graph six level curves of the function f(x, y)=x^{2}y^{2}2 Boost your resume with certification as an expert in up to 15 unique STEM subjects this summer Signup now to start earning your free certificateGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!How to transform the graph of a function?




Level Set Wikipedia




The Graph Below Represents Some Level Curves Of A Chegg Com
Find stepbystep solutions and your answer to the following textbook question Describe the level curves of the function Sketch a contour map of the surface usingLevel surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqA level curve of f ( x, y) is a curve on the domain that satisfies f ( x, y) = k It can be viewed as the intersection of the surface z = f ( x, y) and the horizontal plane z = k projected onto the domain The following diagrams shows how the level curves f ( x, y) = 1 1 − x 2 − y 2 = k changes as k changes



A Predictive Model To Estimate Survival Of Hospitalized Covid 19 Patients From Admission Data Medrxiv



1
These curves are the straight lines in the figure On 6x8y=C, f(x,y)=C The value of C is listed on each level curve in the figure As the plot shows, the function of f(x,y) takes on values between 10 and 10 for points on the circle Hence, the maximum is 10 and the minimum is 10 Note that the maximum and minimum occur at points where theLevel Curves So far we have two methods for visualizing functions arrow diagrams and graphs A third method, borrowed from mapmakers, is a contour map on which points of constant elevation are joined to form contour curves, or level curves A level curve f (x, y) = k is the set of all points in the domain of f at which f takes on a given value kIf the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below Your input find the area between the following curves $$$ y = x^{2} $$$ , $$$ y = \sqrt{x} $$$ on the interval $$$ \left(\infty, \infty\right) $$$
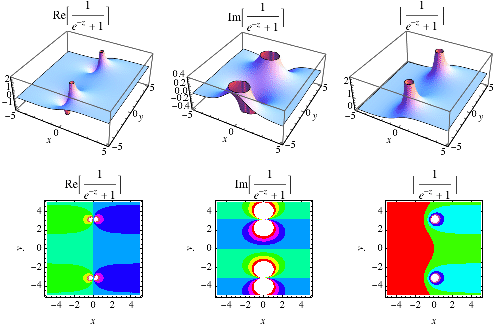



Sigmoid Function From Wolfram Mathworld



2
The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of, the level curves ofGRADIENTS AND LEVEL CURVES There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions inFunctions & Graphing Calculator \square!




Calculus Iii Functions Of Several Variables




Level Curve Calculator All Products Are Discounted Cheaper Than Retail Price Free Delivery Returns Off 68
The level curves of f (x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of c Several of them are shown below One can think of the level curve f (x,y)=c as the horizontal crosssection of the graph at height z=c Plotting 3d graphs and level curves in Matlab I have the following code below, but I cannot test it since I do not have Matlab with me right now and I am afraid I might not have the time to test it by myself when I finally get it I'm trying to plot both 3d graphs and graphs of the level curves in the y and x axis (two dimensions only) ofA level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)



Visualizing Level Curves Geogebra
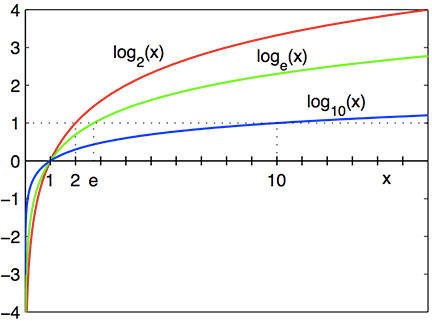



Graphs Of Exponential And Logarithmic Functions Boundless Algebra
Answer and Explanation 1 The level curves of a function f f of two variables are the curves with equations f(x,y) =k f ( x, y) = k , where k k is a constant (in the range of f f ) If you areAnswer to Draw the level curve of the function f(x, y) = x y containing the point (3, 3) By signing up, you'll get thousands of stepbystep I would like to obtain the level curves of a given function z=f(x,y) without using the countours function in the Matlab environment By letting Z equal to some constant 'c' we get a single level curve I would like to obtain an expression of the resulting function of the form y=f(x) to be able to study other properties of it Basic Example 1 Easy game




A Illustrates The Results Of Calculation Of The Additional Displacement Download Scientific Diagram



1
Section 15 Functions of Several Variables In this section we want to go over some of the basic ideas about functions of more than one variable First, remember that graphs of functions of two variables, z = f (x,y) z = f ( x, y) are surfaces in three dimensional space For example, here is the graph of z =2x2 2y2 −4 z = 2 x 2 2 y 2 − 4Y 3 and select the graph of the function a Level curves (Write your answer as an eqeuation that does not involve V) z?Example 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If you




Max Min Of A Curve Learning Hub



Graphing Calculator Math Algebra Calculus Apps On Google Play
By default this expression is x^2 y^2 So if x = 2, and y = 2, z will equal 4 4 = 0 Try hovering over the point (2,2) above You should see in the sidebar that the (x,y,z) indicator displays (2,2,0) So, that explains why we see a contour line along the lineLevel curves Level Curves For a general function z = f(x, y), slicing horizontally is a particularly important idea Level curves for a function z = f(x, y) D ⊆ R2 → R the level curve of value c is the curve C in D ⊆ R2 on which fC = c Notice the critical difference between a level curve C of value c and the trace on the plane zMath Calculus Calculus questions and answers (10) The level curves of a functionſ is shown Use it to estimate the value of (3,2) 170 60 56 40 VO Question (10) The level curves of a functionſ is shown Use it to estimate the value of (3,2) 170 60 56 40 VO
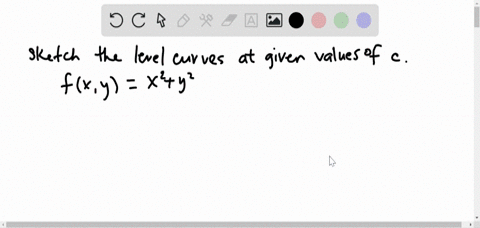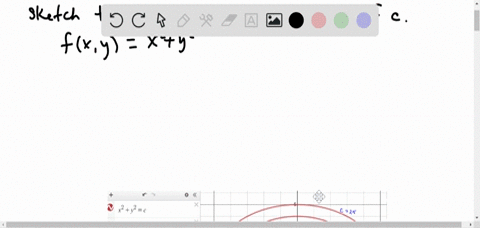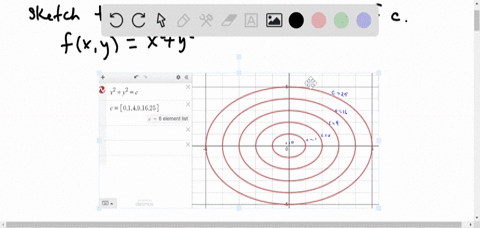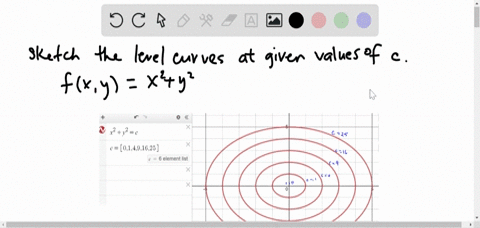



Solved Find And Sketch The Level Curves F X Y C
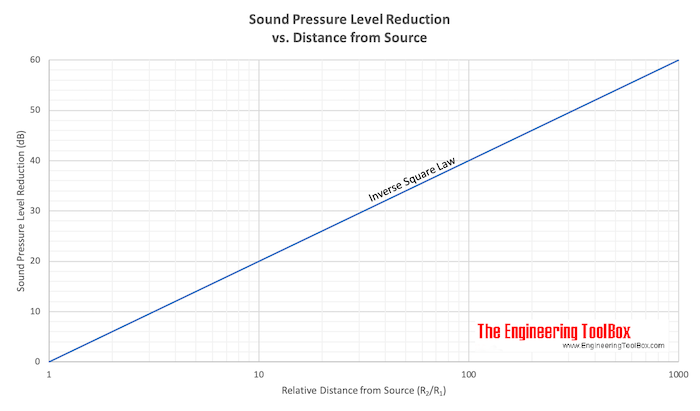



Inverse Square Law Calculator
Curve sketching is a calculation to find all the characteristic points of a function, eg roots, yaxisintercept, maximum and minimum turning points, inflection points How to get those points?




Marginal Utility Formula Calculator Example With Excel Template



Equal Loudness Curves




Level Curves Of The Error Function Download Scientific Diagram




Standard Curve An Overview Sciencedirect Topics




Saddle Point Wikipedia



Sones Phons Loudness Decibel Sone 0 2 0 3 0 4 0 5 0 6 Define Sone Rating Conversion Db Level Dba Phon Phone Volume Intensity Calculator Db Dba And Sone Relate Fan
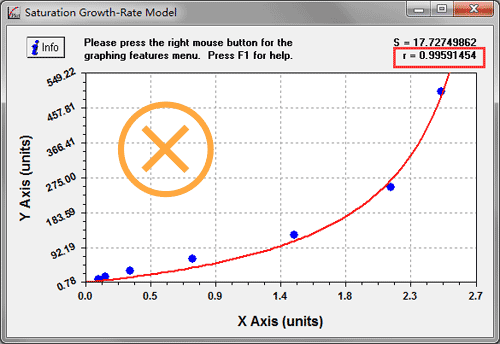



Elisa Data Analysis Cusabio
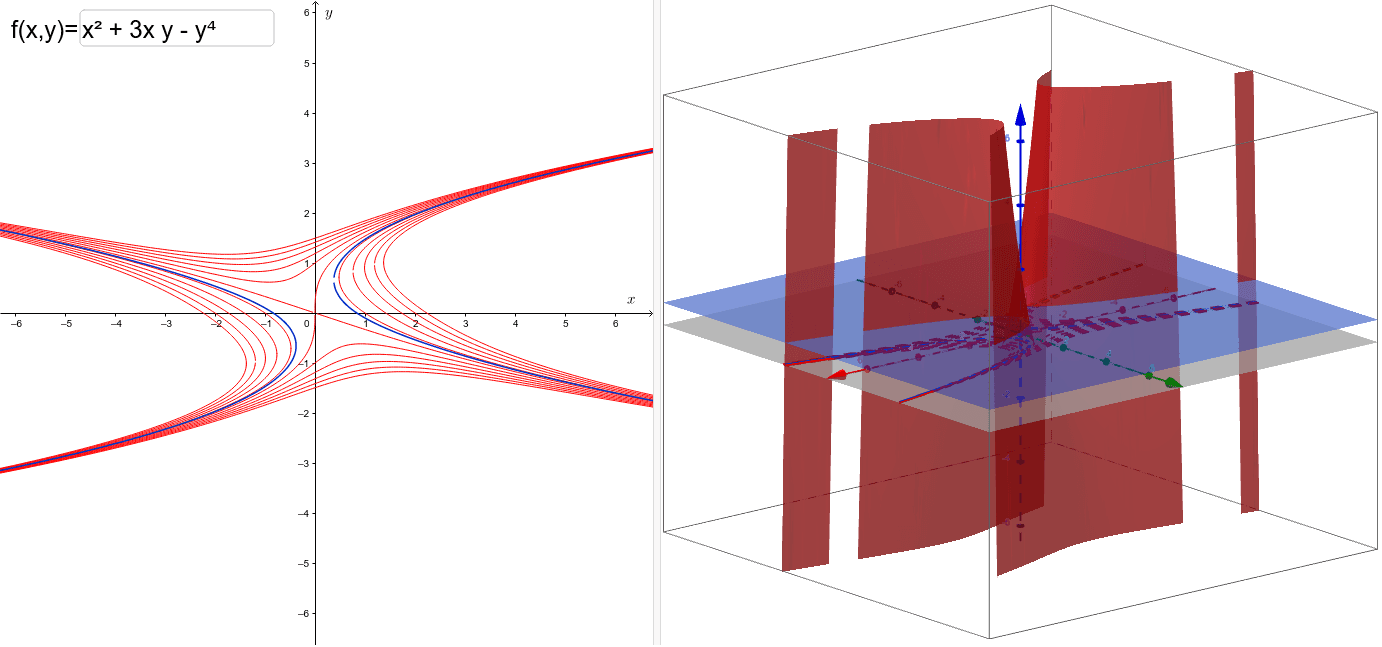



Level Curves Geogebra




Level Set Wikipedia




Mth 254 Test 2 Review Key 0704 Spot Pcc Mth 254 Test 2 Group Review Key Page 2 Of 9 5 I Probably Pdf Document
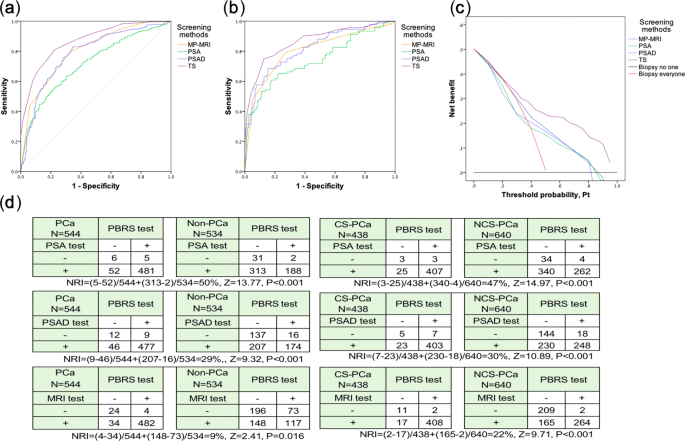



A Calculator Based On Prostate Imaging Reporting And Data System Version 2 Pi Rads V2 Is A Promising Prostate Cancer Predictor Scientific Reports




2 3 Tangent Plane To A Surface Mathematics Libretexts




The 9 Best Graphing Calculators Of 21
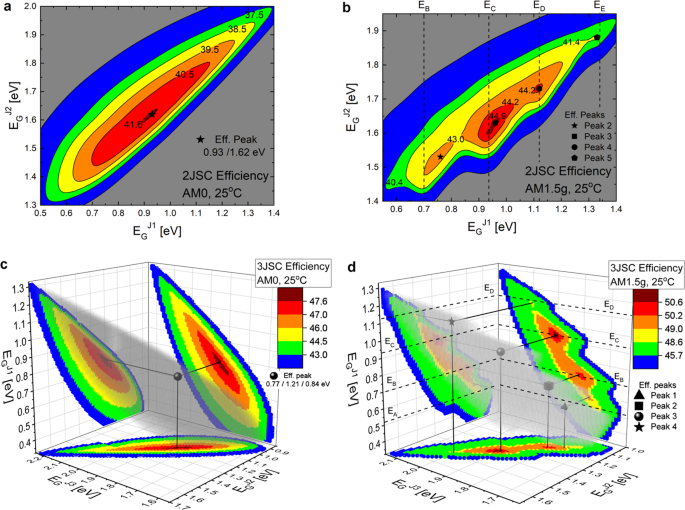



The Influence Of Solar Spectrum And Concentration Factor On The Material Choice And The Efficiency Of Multijunction Solar Cells Scientific Reports



Tpc Auc




Math 148 Exam Iii Practice Problems



Level Curve Calculator All Products Are Discounted Cheaper Than Retail Price Free Delivery Returns Off 68



2
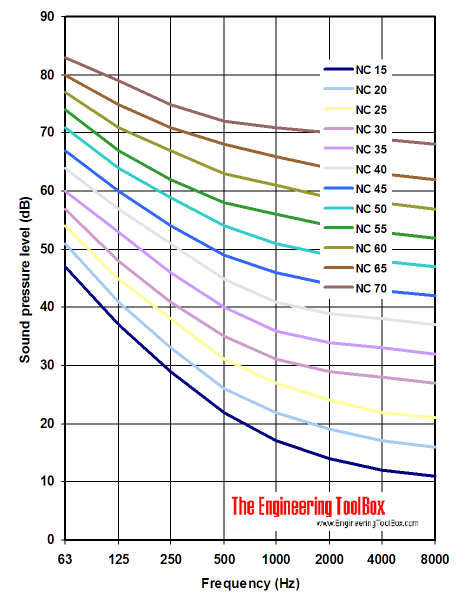



Nc Noise Criterion




Calculation Of Nr Nc Curves In The Optimus Sound Level Meter And The Noisetools Software Pdf Free Download
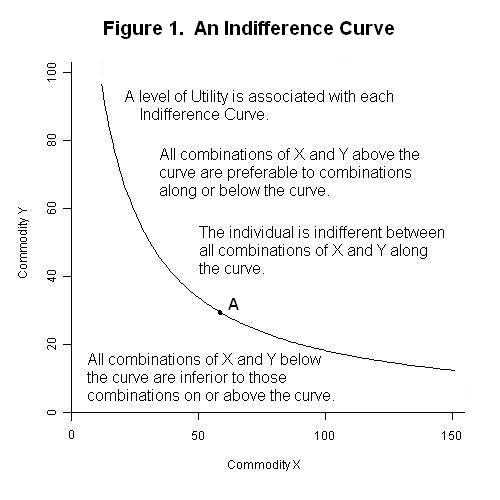



Indifference Curves




Calculus Iii Functions Of Several Variables




Top 7 Uses For A Graphing Calculator Hp Tech Takes
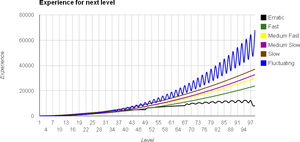



Experience Bulbapedia The Community Driven Pokemon Encyclopedia



Tpc Auc




Analyzing Functions Differential Calculus Math Khan Academy




Level Sets Math Insight




Calculus Iii Functions Of Several Variables




How To Decide Your Sample Size When The Power Calculation Is Not Straightforward Nc3rs




Level Curves




Level Curves Of Functions Of Two Variables Youtube




Desmos Review For Teachers Common Sense Education
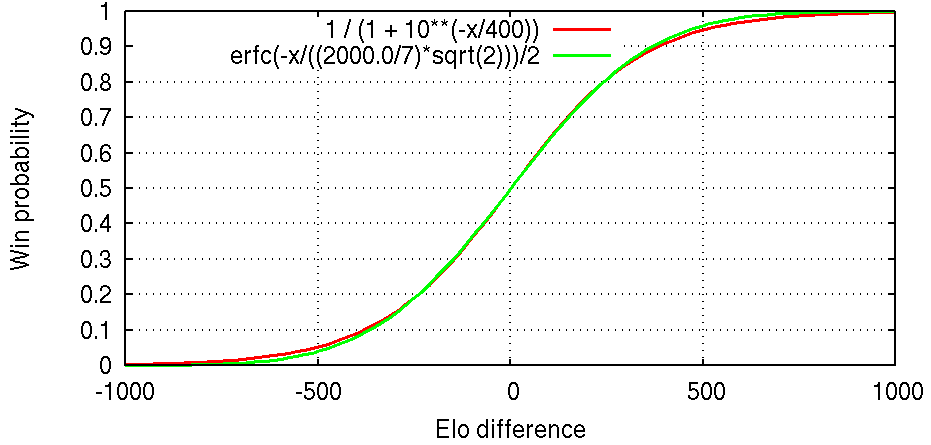



Elo Win Probability Calculator




How To Sketch Level Curves Youtube




Example 11 Sketch The Level Curves Of The Function Chegg Com




Level Curves For The Region Of The Potential Energy Surface With The Download Scientific Diagram




Level Sets Math Insight



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang Pdf



Desmos Accessibility
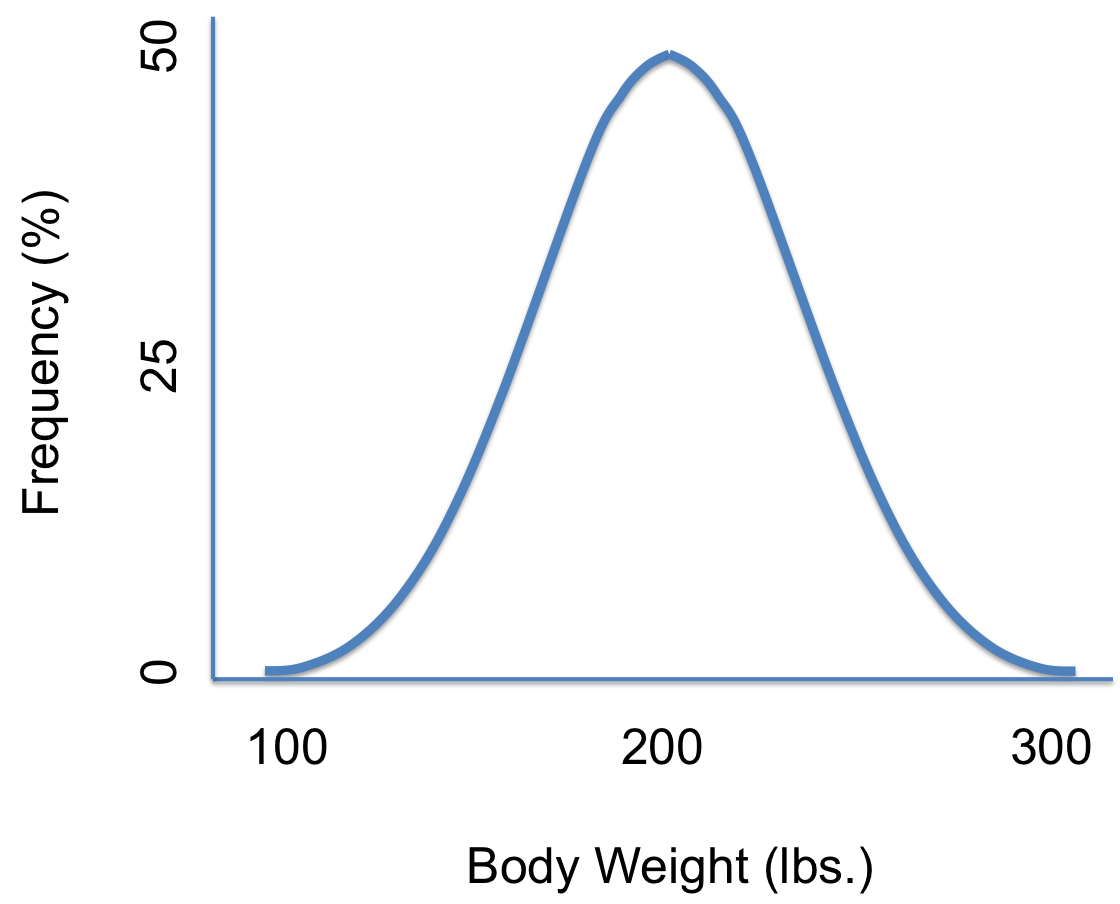



Density Curve Examples Statistics How To




Sample Questions Exam 2 Calculus Iii Math 275 Docsity



1




Practice Quiz 5 Multivariable And Vector Calculus Math 275 Docsity
/ScreenShot2020-02-11at12.52.56PM-a9175650691c48c18cdff16e42fdb830.png)



The 9 Best Graphing Calculators Of 21



Graphing Calculator Math Algebra Calculus Apps On Google Play



Equal Loudness Curves




Level Curves Of Function At Z 0 Mathematics Stack Exchange




M1c Exam1 Notes F14
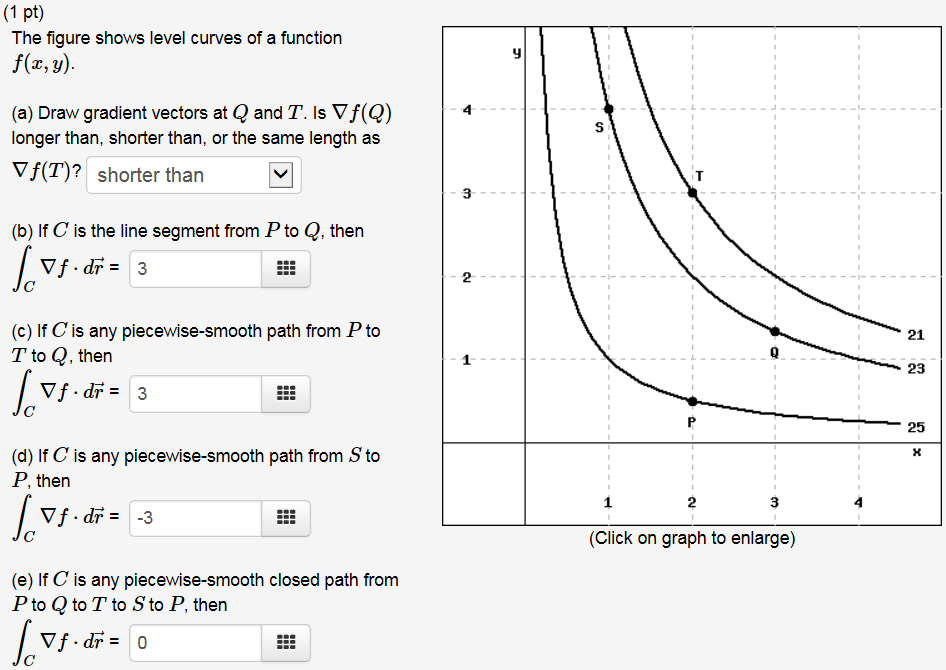



The Figure Shows Level Curves Of A Function F X Y Chegg Com



Sample Size Calculation Area Under Roc Curve



Experience Bulbapedia The Community Driven Pokemon Encyclopedia



Level Curves




Amazon Com Casio Prizm Fx Cg50 Color Graphing Calculator Electronics




Level Sets Math Insight




The Figure Shows Level Curves Of A Function F In The Square R 0 6 Times 0 6 Use The Midpoint Rule With M N 2 To Estimate



Contour Plotter Academo Org Free Interactive Education
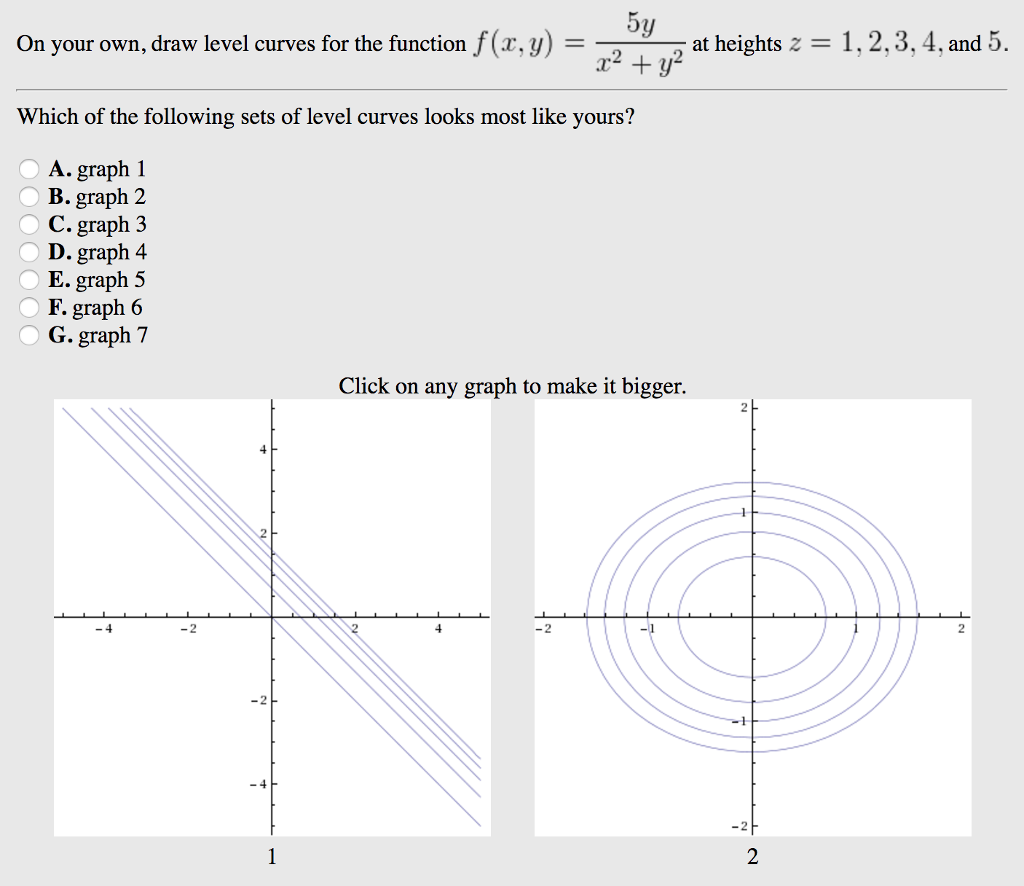



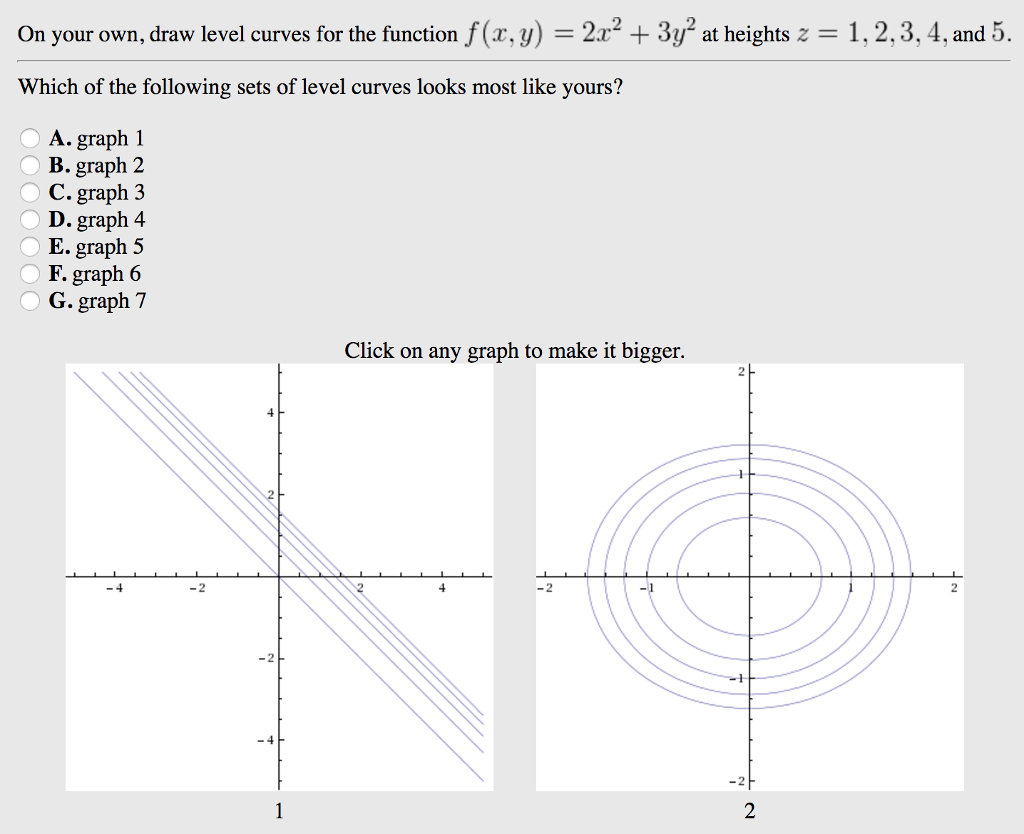
On Your Own Draw Level Curves For The Function F A Chegg Com




Beta Distribution Chart Calculator High Accuracy Calculation



Visualizing Level Curves Geogebra




Amazon Com Casio Prizm Fx Cg50 Color Graphing Calculator Electronics



2
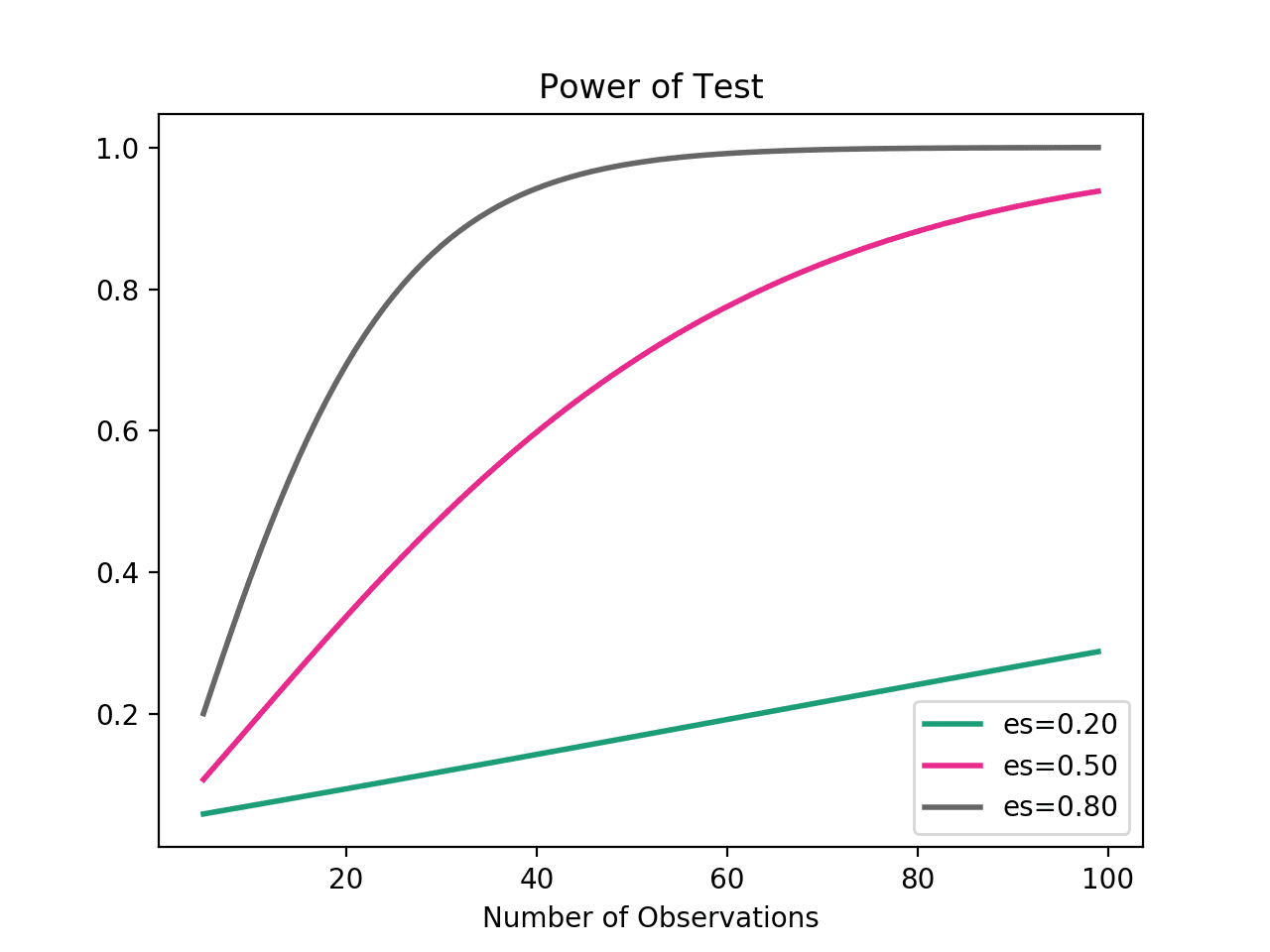



A Gentle Introduction To Statistical Power And Power Analysis In Python




If It Is Exact Find A Function F X Y Whose Differential Df X Y Gives The Differential Equation Brainly Com



Graphing Calculator Symbolab




Calc Iii Contour Map Level Curves Youtube
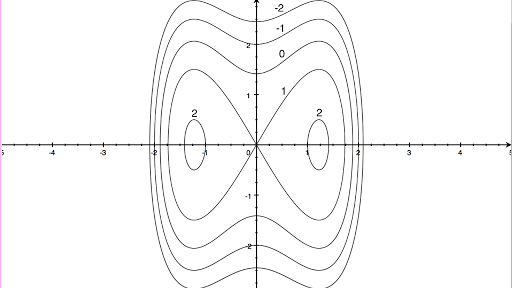



Contour Maps Article Khan Academy
:max_bytes(150000):strip_icc()/marginal_rate_of_substitution_final2-893aa48189714fcb97dadb6f97b03948.png)



Isoquant Curve Definition
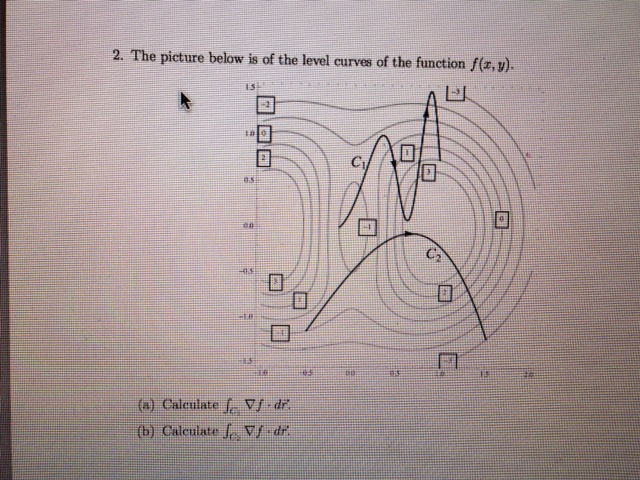



Solved The Picture Below Is Of The Level Curves Of The Fu Chegg Com




Data Logging And Cooling Curves Casioed




Graphing Level Curves Mathematics Stack Exchange




14 1 Functions Of Several Variables Mathematics Libretexts
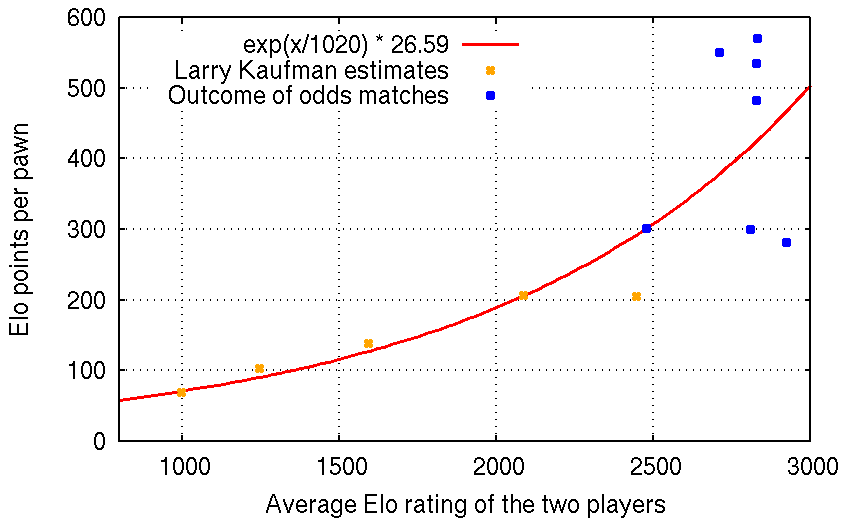



Elo Win Probability Calculator



Dba Weighting Filter Frequency To Dba And Dbc Db A And Db C A Weighted Sound Calculate Din Iec 651 Calculator Equal Loudness Contours Sengpielaudio Sengpiel Berlin




Graphs Of Square Root Functions Ck 12 Foundation



2
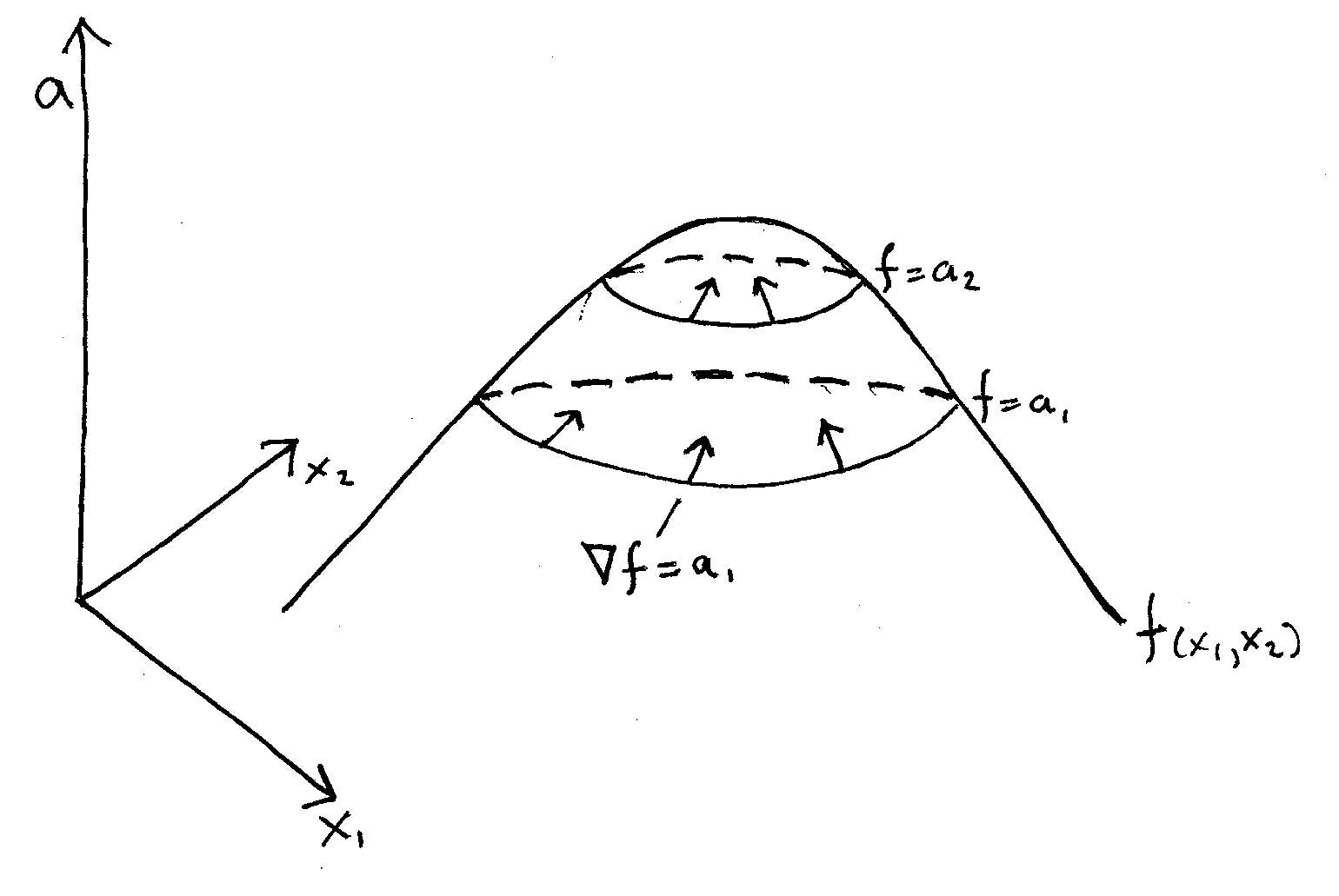



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium




Level Curves




Partial Derivative Calculator Xyz Assignment For Partial Derivative Calculate With Analytic Geometry Iii Mat 272 Docsity This Online Calculator Will Calculate The Partial Derivative Of The Function With Steps Shown



0 件のコメント:
コメントを投稿